Partial Sums

4000ms

262144K

Description:

You've got an array a, consisting of n integers. The array elements are indexed from 1 to n. Let's determine a two step operation like that:

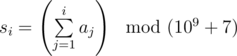First we build by the array a an array s of partial sums, consisting of n elements. Element number i (1 ≤ i ≤ n) of array s equals $\text{[math]}$ . The operation x mod y means that we take the remainder of the division of number x by number y.
Then we write the contents of the array s to the array a. Element number i (1 ≤ i ≤ n) of the array s becomes the i-th element of the array a (a_i = s_i).

You task is to find array a after exactly k described operations are applied.

Input:

The first line contains two space-separated integers n and k (1 ≤ n ≤ 2000, 0 ≤ k ≤ 10⁹). The next line contains n space-separated integers a₁, a₂, ..., a_n — elements of the array a (0 ≤ a_i ≤ 10⁹).

Output:

Print n integers — elements of the array a after the operations are applied to it. Print the elements in the order of increasing of their indexes in the array a. Separate the printed numbers by spaces.

Sample Input:

3 1
1 2 3

Sample Output:

1 3 6

Sample Input:

5 0
3 14 15 92 6

Sample Output:

3 14 15 92 6

Informação

Provedor Codeforces

Código CF223C