Not Wool Sequences

1000ms

262144K

Description:

A sequence of non-negative integers a₁, a₂, ..., a_n of length n is called a wool sequence if and only if there exists two integers l and r (1 ≤ l ≤ r ≤ n) such that $\text{[math]}$ . In other words each wool sequence contains a subsequence of consecutive elements with xor equal to 0.

The expression 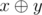$\text{[math]}$ means applying the operation of a bitwise xor to numbers x and y. The given operation exists in all modern programming languages, for example, in languages C++ and Java it is marked as "^", in Pascal — as "xor".

In this problem you are asked to compute the number of sequences made of n integers from 0 to 2^m - 1 that are not a wool sequence. You should print this number modulo 1000000009 (10⁹ + 9).

Input:

The only line of input contains two space-separated integers n and m (1 ≤ n, m ≤ 10⁵).

Output:

Print the required number of sequences modulo 1000000009 (10⁹ + 9) on the only line of output.

Sample Input:

3 2

Sample Output:

Note:

Sequences of length 3 made of integers 0, 1, 2 and 3 that are not a wool sequence are (1, 3, 1), (1, 2, 1), (2, 1, 2), (2, 3, 2), (3, 1, 3) and (3, 2, 3).

Informação

Provedor Codeforces

Código CF238A