Maxim and Increasing Subsequence

6000ms

262144K

Description:

Maxim loves sequences, especially those that strictly increase. He is wondering, what is the length of the longest increasing subsequence of the given sequence a?

Sequence a is given as follows:

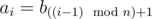the length of the sequence equals n × t;
$\text{[math]}$ (1 ≤ i ≤ n × t), where operation 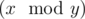$\text{[math]}$ means taking the remainder after dividing number x by number y.

Sequence s₁, s₂, ..., s_r of length r is a subsequence of sequence a₁, a₂, ..., a_n, if there is such increasing sequence of indexes i₁, i₂, ..., i_r (1 ≤ i₁ < i₂ < ... < i_r ≤ n), that a_{i_j} = s_j. In other words, the subsequence can be obtained from the sequence by crossing out some elements.

Sequence s₁, s₂, ..., s_r is increasing, if the following inequality holds: s₁ < s₂ < ... < s_r.

Maxim have k variants of the sequence a. Help Maxim to determine for each sequence the length of the longest increasing subsequence.

Input:

The first line contains four integers k, n, maxb and t (1 ≤ k ≤ 10; 1 ≤ n, maxb ≤ 10⁵; 1 ≤ t ≤ 10⁹; n × maxb ≤ 2·10⁷). Each of the next k lines contain n integers b₁, b₂, ..., b_n (1 ≤ b_i ≤ maxb).

Note that for each variant of the sequence a the values n, maxb and t coincide, the only arrays bs differ.

The numbers in the lines are separated by single spaces.

Output:

Print k integers — the answers for the variants of the sequence a. Print the answers in the order the variants follow in the input.

Sample Input:

Sample Output:

2
3
3

Informação

Provedor Codeforces

Código CF261D