Find Maximum

1000ms

262144K

Description:

Valera has array a, consisting of n integers a₀, a₁, ..., a_n - 1, and function f(x), taking an integer from 0 to 2ⁿ - 1 as its single argument. Value f(x) is calculated by formula 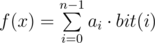$\text{[math]}$ , where value bit(i) equals one if the binary representation of number x contains a 1 on the i-th position, and zero otherwise.

For example, if n = 4 and x = 11 (11 = 2⁰ + 2¹ + 2³), then f(x) = a₀ + a₁ + a₃.

Help Valera find the maximum of function f(x) among all x, for which an inequality holds: 0 ≤ x ≤ m.

Input:

The first line contains integer n (1 ≤ n ≤ 10⁵) — the number of array elements. The next line contains n space-separated integers a₀, a₁, ..., a_n - 1 (0 ≤ a_i ≤ 10⁴) — elements of array a.

The third line contains a sequence of digits zero and one without spaces s₀s₁... s_n - 1 — the binary representation of number m. Number m equals 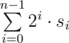$\text{[math]}$ .

Output:

Print a single integer — the maximum value of function f(x) for all 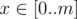$\text{[math]}$ .

Sample Input:

2
3 8
10

Sample Output:

Sample Input:

5
17 0 10 2 1
11010

Sample Output:

Note:

In the first test case m = 2⁰ = 1, f(0) = 0, f(1) = a₀ = 3.

In the second sample m = 2⁰ + 2¹ + 2³ = 11, the maximum value of function equals f(5) = a₀ + a₂ = 17 + 10 = 27.

Informação

Provedor Codeforces

Código CF353C