Bear and Prime Numbers

2000ms

524288K

Description:

Recently, the bear started studying data structures and faced the following problem.

You are given a sequence of integers x₁, x₂, ..., x_n of length n and m queries, each of them is characterized by two integers l_i, r_i. Let's introduce f(p) to represent the number of such indexes k, that x_k is divisible by p. The answer to the query l_i, r_i is the sum: 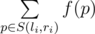$\text{[math]}$ , where S(l_i, r_i) is a set of prime numbers from segment [l_i, r_i] (both borders are included in the segment).

Help the bear cope with the problem.

Input:

The first line contains integer n (1 ≤ n ≤ 10⁶). The second line contains n integers x₁, x₂, ..., x_n (2 ≤ x_i ≤ 10⁷). The numbers are not necessarily distinct.

The third line contains integer m (1 ≤ m ≤ 50000). Each of the following m lines contains a pair of space-separated integers, l_i and r_i (2 ≤ l_i ≤ r_i ≤ 2·10⁹) — the numbers that characterize the current query.

Output:

Print m integers — the answers to the queries on the order the queries appear in the input.

Sample Input:

6
5 5 7 10 14 15
3
2 11
3 12
4 4

Sample Output:

9
7
0

Sample Input:

7
2 3 5 7 11 4 8
2
8 10
2 123

Sample Output:

0
7

Note:

Consider the first sample. Overall, the first sample has 3 queries.

The first query l = 2, r = 11 comes. You need to count f(2) + f(3) + f(5) + f(7) + f(11) = 2 + 1 + 4 + 2 + 0 = 9.
The second query comes l = 3, r = 12. You need to count f(3) + f(5) + f(7) + f(11) = 1 + 4 + 2 + 0 = 7.
The third query comes l = 4, r = 4. As this interval has no prime numbers, then the sum equals 0.

Informação

Provedor Codeforces

Código CF385C