Dima and Bacteria

2000ms

262144K

Description:

Dima took up the biology of bacteria, as a result of his experiments, he invented k types of bacteria. Overall, there are n bacteria at his laboratory right now, and the number of bacteria of type i equals c_i. For convenience, we will assume that all the bacteria are numbered from 1 to n. The bacteria of type c_i are numbered from 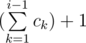$\text{[math]}$ to $\text{[math]}$ .

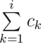With the help of special equipment Dima can move energy from some bacteria into some other one. Of course, the use of such equipment is not free. Dima knows m ways to move energy from some bacteria to another one. The way with number i can be described with integers u_i, v_i and x_i mean that this way allows moving energy from bacteria with number u_i to bacteria with number v_i or vice versa for x_i dollars.

Dima's Chef (Inna) calls the type-distribution correct if there is a way (may be non-direct) to move energy from any bacteria of the particular type to any other bacteria of the same type (between any two bacteria of the same type) for zero cost.

As for correct type-distribution the cost of moving the energy depends only on the types of bacteria help Inna to determine is the type-distribution correct? If it is, print the matrix d with size k × k. Cell d[i][j] of this matrix must be equal to the minimal possible cost of energy-moving from bacteria with type i to bacteria with type j.

Input:

The first line contains three integers n, m, k (1 ≤ n ≤ 10⁵; 0 ≤ m ≤ 10⁵; 1 ≤ k ≤ 500). The next line contains k integers c₁, c₂, ..., c_k (1 ≤ c_i ≤ n). Each of the next m lines contains three integers u_i, v_i, x_i (1 ≤ u_i, v_i ≤ 10⁵; 0 ≤ x_i ≤ 10⁴). It is guaranteed that 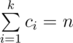$\text{[math]}$ .

Output:

If Dima's type-distribution is correct, print string «Yes», and then k lines: in the i-th line print integers d[i][1], d[i][2], ..., d[i][k] (d[i][i] = 0). If there is no way to move energy from bacteria i to bacteria j appropriate d[i][j] must equal to -1. If the type-distribution isn't correct print «No».

Sample Input:

Sample Output:

Yes
0 2
2 0

Sample Input:

3 1 2
2 1
1 2 0

Sample Output:

Yes
0 -1
-1 0

Sample Input:

Sample Output:

Yes
0 1
1 0

Sample Input:

3 0 2
1 2

Sample Output:

No

Informação

Provedor Codeforces

Código CF400D