Searching for Graph

1000ms

262144K

Description:

Let's call an undirected graph of n vertices p-interesting, if the following conditions fulfill:

the graph contains exactly 2n + p edges;
the graph doesn't contain self-loops and multiple edges;
for any integer k (1 ≤ k ≤ n), any subgraph consisting of k vertices contains at most 2k + p edges.

A subgraph of a graph is some set of the graph vertices and some set of the graph edges. At that, the set of edges must meet the condition: both ends of each edge from the set must belong to the chosen set of vertices.

Your task is to find a p-interesting graph consisting of n vertices.

Input:

The first line contains a single integer t (1 ≤ t ≤ 5) — the number of tests in the input. Next t lines each contains two space-separated integers: n, p (5 ≤ n ≤ 24; p ≥ 0; 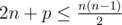$\text{[math]}$ ) — the number of vertices in the graph and the interest value for the appropriate test.

It is guaranteed that the required graph exists.

Output:

For each of the t tests print 2n + p lines containing the description of the edges of a p-interesting graph: the i-th line must contain two space-separated integers a_i, b_i (1 ≤ a_i, b_i ≤ n; a_i ≠ b_i) — two vertices, connected by an edge in the resulting graph. Consider the graph vertices numbered with integers from 1 to n.

Print the answers to the tests in the order the tests occur in the input. If there are multiple solutions, you can print any of them.

Sample Input:

1
6 0

Sample Output:

Informação

Provedor Codeforces

Código CF402C