Tree

2000ms

262144K

Description:

Little X has a tree consisting of n nodes (they are numbered from 1 to n). Each edge of the tree has a positive length. Let's define the distance between two nodes v and u (we'll denote it d(v, u)) as the sum of the lengths of edges in the shortest path between v and u.

A permutation p is a sequence of n distinct integers p₁, p₂, ..., p_n (1 ≤ p_i ≤ n). Little X wants to find a permutation p such that sum 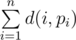$\text{[math]}$ is maximal possible. If there are multiple optimal permutations, he wants to find the lexicographically smallest one. Help him with the task!

Input:

The first line contains an integer n (1 ≤ n ≤ 10⁵).

Each of the next n - 1 lines contains three space separated integers u_i, v_i, w_i (1 ≤ u_i, v_i ≤ n; 1 ≤ w_i ≤ 10⁵), denoting an edge between nodes u_i and v_i with length equal to w_i.

It is guaranteed that these edges form a tree.

Output:

In the first line print the maximum possible value of the described sum. In the second line print n integers, representing the lexicographically smallest permutation.

Sample Input:

2
1 2 3

Sample Output:

6
2 1

Sample Input:

Sample Output:

32
2 1 4 5 3

Informação

Provedor Codeforces

Código CF468D