Drazil and His Happy Friends

4000ms

262144K

Description:

Drazil has many friends. Some of them are happy and some of them are unhappy. Drazil wants to make all his friends become happy. So he invented the following plan.

There are n boys and m girls among his friends. Let's number them from 0 to n - 1 and 0 to m - 1 separately. In i-th day, Drazil invites 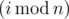$\text{[math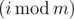]}$ -th boy and $\text{[math]}$ -th girl to have dinner together (as Drazil is programmer, i starts from 0). If one of those two people is happy, the other one will also become happy. Otherwise, those two people remain in their states. Once a person becomes happy (or if it is happy originally), he stays happy forever.

Drazil wants to know on which day all his friends become happy or to determine if they won't become all happy at all.

Input:

The first line contains two integer n and m (1 ≤ n, m ≤ 10⁹).

The second line contains integer b (0 ≤ b ≤ min(n, 10⁵)), denoting the number of happy boys among friends of Drazil, and then follow b distinct integers x₁, x₂, ..., x_b (0 ≤ x_i < n), denoting the list of indices of happy boys.

The third line conatins integer g (0 ≤ g ≤ min(m, 10⁵)), denoting the number of happy girls among friends of Drazil, and then follow g distinct integers y₁, y₂, ... , y_g (0 ≤ y_j < m), denoting the list of indices of happy girls.

It is guaranteed that there is at least one person that is unhappy among his friends.

Output:

Print the number of the first day that all friends of Drazil become happy. If this day won't come at all, you print -1.

Sample Input:

2 3
0
1 0

Sample Output:

Sample Input:

2 4
1 0
1 2

Sample Output:

-1

Sample Input:

2 3
1 0
1 1

Sample Output:

Sample Input:

99999 100000
2 514 415
2 50216 61205

Sample Output:

4970100515

Note:

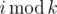By $\text{[math]}$ we define the remainder of integer division of i by k.

In first sample case:

On the 0-th day, Drazil invites 0-th boy and 0-th girl. Because 0-th girl is happy at the beginning, 0-th boy become happy at this day.
On the 1-st day, Drazil invites 1-st boy and 1-st girl. They are both unhappy, so nothing changes at this day.
On the 2-nd day, Drazil invites 0-th boy and 2-nd girl. Because 0-th boy is already happy he makes 2-nd girl become happy at this day.
On the 3-rd day, Drazil invites 1-st boy and 0-th girl. 0-th girl is happy, so she makes 1-st boy happy.
On the 4-th day, Drazil invites 0-th boy and 1-st girl. 0-th boy is happy, so he makes the 1-st girl happy. So, all friends become happy at this moment.

Informação

Provedor Codeforces

Código CF516E