Preparando MOJI
Tavas lives in Tavaspolis. Tavaspolis has n cities numbered from 1 to n connected by n - 1 bidirectional roads. There exists a path between any two cities. Also each road has a length.
Tavas' favorite strings are binary strings (they contain only 0 and 1). For any binary string like s = s1s2... sk, T(s) is its Goodness. T(s) can be calculated as follows:
Consider there are exactly m blocks of 1s in this string (a block of 1s in s is a maximal consecutive substring of s that only contains 1) with lengths x1, x2, ..., xm.
Define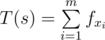 
where f is a given sequence (if m = 0, then T(s) = 0).
Tavas loves queries. He asks you to answer q queries. In each query he gives you numbers v, u, l and you should print following number:
Consider the roads on the path from city v to city u: e1, e2, ..., ex.
Build the binary string b of length x such that: bi = 1 if and only if l ≤ w(ei) where w(e) is the length of road e.
You should print T(b) for this query.
The first line of input contains integers n and q (2 ≤ n ≤ 105 and 1 ≤ q ≤ 105).
The next line contains n - 1 space separated integers f1, f2, ..., fn - 1 (|fi| ≤ 1000).
The next n - 1 lines contain the details of the roads. Each line contains integers v, u and w and it means that there's a road between cities v and u of length w (1 ≤ v, u ≤ n and 1 ≤ w ≤ 109).
The next q lines contain the details of the queries. Each line contains integers v, u, l (1 ≤ v, u ≤ n, v ≠ u and 1 ≤ l ≤ 109).
Print the answer of each query in a single line.
2 3
10
1 2 3
1 2 2
1 2 3
1 2 4
10
10
0
6 6
-5 0 0 2 10
1 2 1
2 3 2
3 4 5
4 5 1
5 6 5
1 6 1
1 6 2
1 6 5
3 6 5
4 6 4
1 4 2
10
-5
-10
-10
-5
0
Informação
Provedor Codeforces
Código CF536E
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 08:57:38
Relacionados