Preparando MOJI
Some time ago Leonid have known about idempotent functions. Idempotent function defined on a set {1, 2, ..., n} is such function 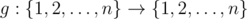 , that for any
, that for any 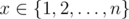 the formula g(g(x)) = g(x) holds.
the formula g(g(x)) = g(x) holds.
Let's denote as f(k)(x) the function f applied k times to the value x. More formally, f(1)(x) = f(x), f(k)(x) = f(f(k - 1)(x)) for each k > 1.
You are given some function 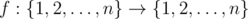 . Your task is to find minimum positive integer k such that function f(k)(x) is idempotent.
. Your task is to find minimum positive integer k such that function f(k)(x) is idempotent.
In the first line of the input there is a single integer n (1 ≤ n ≤ 200) — the size of function f domain.
In the second line follow f(1), f(2), ..., f(n) (1 ≤ f(i) ≤ n for each 1 ≤ i ≤ n), the values of a function.
Output minimum k such that function f(k)(x) is idempotent.
4
1 2 2 4
1
3
2 3 3
2
3
2 3 1
3
In the first sample test function f(x) = f(1)(x) is already idempotent since f(f(1)) = f(1) = 1, f(f(2)) = f(2) = 2, f(f(3)) = f(3) = 2, f(f(4)) = f(4) = 4.
In the second sample test:
In the third sample test:
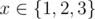 meaning that the formula f(3)(f(3)(x)) = f(3)(x) also holds.
meaning that the formula f(3)(f(3)(x)) = f(3)(x) also holds.