A Museum Robbery

2000ms

262144K

Description:

There's a famous museum in the city where Kleofáš lives. In the museum, n exhibits (numbered 1 through n) had been displayed for a long time; the i-th of those exhibits has value v_i and mass w_i.

Then, the museum was bought by a large financial group and started to vary the exhibits. At about the same time, Kleofáš... gained interest in the museum, so to say.

You should process q events of three types:

type 1 — the museum displays an exhibit with value v and mass w; the exhibit displayed in the i-th event of this type is numbered n + i (see sample explanation for more details)
type 2 — the museum removes the exhibit with number x and stores it safely in its vault
type 3 — Kleofáš visits the museum and wonders (for no important reason at all, of course): if there was a robbery and exhibits with total mass at most m were stolen, what would their maximum possible total value be?

For each event of type 3, let s(m) be the maximum possible total value of stolen exhibits with total mass ≤ m.

Formally, let D be the set of numbers of all exhibits that are currently displayed (so initially D = {1, ..., n}). Let P(D) be the set of all subsets of D and let

$\text{[math]}$

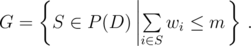
Then, s(m) is defined as

$\text{[math]}$

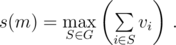
Compute s(m) for each 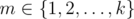$\text{[math]}$ . Note that the output follows a special format.

Input:

The first line of the input contains two space-separated integers n and k (1 ≤ n ≤ 5000, 1 ≤ k ≤ 1000) — the initial number of exhibits in the museum and the maximum interesting mass of stolen exhibits.

Then, n lines follow. The i-th of them contains two space-separated positive integers v_i and w_i (1 ≤ v_i ≤ 1 000 000, 1 ≤ w_i ≤ 1000) — the value and mass of the i-th exhibit.

The next line contains a single integer q (1 ≤ q ≤ 30 000) — the number of events.

Each of the next q lines contains the description of one event in the following format:

1 v w — an event of type 1, a new exhibit with value v and mass w has been added (1 ≤ v ≤ 1 000 000, 1 ≤ w ≤ 1000)
2 x — an event of type 2, the exhibit with number x has been removed; it's guaranteed that the removed exhibit had been displayed at that time
3 — an event of type 3, Kleofáš visits the museum and asks his question

There will be at most 10 000 events of type 1 and at least one event of type 3.

Output:

As the number of values s(m) can get large, output the answers to events of type 3 in a special format.

For each event of type 3, consider the values s(m) computed for the question that Kleofáš asked in this event; print one line containing a single number

$\text{[math]}$

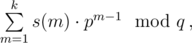
where p = 10⁷ + 19 and q = 10⁹ + 7.

Print the answers to events of type 3 in the order in which they appear in the input.

Sample Input:

Sample Output:

Sample Input:

Sample Output:

Note:

In the first sample, the numbers of displayed exhibits and values s(1), ..., s(10) for individual events of type 3 are, in order:

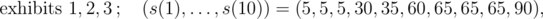
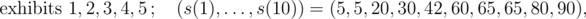
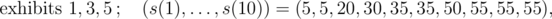
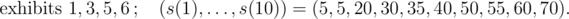
$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

The values of individual exhibits are v₁ = 30, v₂ = 60, v₃ = 5, v₄ = 42, v₅ = 20, v₆ = 40 and their masses are w₁ = 4, w₂ = 6, w₃ = 1, w₄ = 5, w₅ = 3, w₆ = 6.

In the second sample, the only question is asked after removing all exhibits, so s(m) = 0 for any m.

Informação

Provedor Codeforces

Código CF601E