Moodular Arithmetic

1000ms

262144K

Description:

As behooves any intelligent schoolboy, Kevin Sun is studying psycowlogy, cowculus, and cryptcowgraphy at the Bovinia State University (BGU) under Farmer Ivan. During his Mathematics of Olympiads (MoO) class, Kevin was confronted with a weird functional equation and needs your help. For two fixed integers k and p, where p is an odd prime number, the functional equation states that

$\text{[math]}$

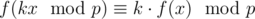
for some function 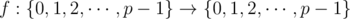$\text{[math]}$ . (This equation should hold for any integer x in the range 0 to p - 1, inclusive.)

It turns out that f can actually be many different functions. Instead of finding a solution, Kevin wants you to count the number of distinct functions f that satisfy this equation. Since the answer may be very large, you should print your result modulo 10⁹ + 7.

Input:

The input consists of two space-separated integers p and k (3 ≤ p ≤ 1 000 000, 0 ≤ k ≤ p - 1) on a single line. It is guaranteed that p is an odd prime number.

Output:

Print a single integer, the number of distinct functions f modulo 10⁹ + 7.

Sample Input:

3 2

Sample Output:

Sample Input:

5 4

Sample Output:

Note:

In the first sample, p = 3 and k = 2. The following functions work:

f(0) = 0, f(1) = 1, f(2) = 2.
f(0) = 0, f(1) = 2, f(2) = 1.
f(0) = f(1) = f(2) = 0.

Informação

Provedor Codeforces

Código CF603B