Bear and Bad Powers of 42

5000ms

262144K

Description:

Limak, a bear, isn't good at handling queries. So, he asks you to do it.

We say that powers of 42 (numbers 1, 42, 1764, ...) are bad. Other numbers are good.

You are given a sequence of n good integers t₁, t₂, ..., t_n. Your task is to handle q queries of three types:

1 i — print t_i in a separate line.
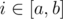2 a b x — for $\text{[math]}$ set t_i to x. It's guaranteed that x is a good number.
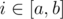3 a b x — for $\text{[math]}$ increase t_i by x. After this repeat the process while at least one t_i is bad.

You can note that after each query all t_i are good.

Input:

The first line of the input contains two integers n and q (1 ≤ n, q ≤ 100 000) — the size of Limak's sequence and the number of queries, respectively.

The second line of the input contains n integers t₁, t₂, ..., t_n (2 ≤ t_i ≤ 10⁹) — initial elements of Limak's sequence. All t_i are good.

Then, q lines follow. The i-th of them describes the i-th query. The first number in the line is an integer type_i (1 ≤ type_i ≤ 3) — the type of the query. There is at least one query of the first type, so the output won't be empty.

In queries of the second and the third type there is 1 ≤ a ≤ b ≤ n.

In queries of the second type an integer x (2 ≤ x ≤ 10⁹) is guaranteed to be good.

In queries of the third type an integer x (1 ≤ x ≤ 10⁹) may be bad.

Output:

For each query of the first type, print the answer in a separate line.

Sample Input:

6 12
40 1700 7 1672 4 1722
3 2 4 42
1 2
1 3
3 2 6 50
1 2
1 4
1 6
2 3 4 41
3 1 5 1
1 1
1 3
1 5

Sample Output:

Note:

After a query 3 2 4 42 the sequence is 40, 1742, 49, 1714, 4, 1722.

After a query 3 2 6 50 the sequence is 40, 1842, 149, 1814, 104, 1822.

After a query 2 3 4 41 the sequence is 40, 1842, 41, 41, 104, 1822.

After a query 3 1 5 1 the sequence is 43, 1845, 44, 44, 107, 1822.

Informação

Provedor Codeforces

Código CF679E