Ant Man

4000ms

262144K

Description:

Scott Lang is at war with Darren Cross. There are n chairs in a hall where they are, numbered with 1, 2, ..., n from left to right. The i-th chair is located at coordinate x_i. Scott is on chair number s and Cross is on chair number e. Scott can jump to all other chairs (not only neighboring chairs). He wants to start at his position (chair number s), visit each chair exactly once and end up on chair number e with Cross.

As we all know, Scott can shrink or grow big (grow big only to his normal size), so at any moment of time he can be either small or large (normal). The thing is, he can only shrink or grow big while being on a chair (not in the air while jumping to another chair). Jumping takes time, but shrinking and growing big takes no time. Jumping from chair number i to chair number j takes |x_i - x_j| seconds. Also, jumping off a chair and landing on a chair takes extra amount of time.

If Scott wants to jump to a chair on his left, he can only be small, and if he wants to jump to a chair on his right he should be large.

Jumping off the i-th chair takes:

c_i extra seconds if he's small.
d_i extra seconds otherwise (he's large).

Also, landing on i-th chair takes:

b_i extra seconds if he's small.
a_i extra seconds otherwise (he's large).

In simpler words, jumping from i-th chair to j-th chair takes exactly:

|x_i - x_j| + c_i + b_j seconds if j < i.
|x_i - x_j| + d_i + a_j seconds otherwise (j > i).

Given values of x, a, b, c, d find the minimum time Scott can get to Cross, assuming he wants to visit each chair exactly once.

Input:

The first line of the input contains three integers n, s and e (2 ≤ n ≤ 5000, 1 ≤ s, e ≤ n, s ≠ e) — the total number of chairs, starting and ending positions of Scott.

The second line contains n integers x₁, x₂, ..., x_n (1 ≤ x₁ < x₂ < ... < x_n ≤ 10⁹).

The third line contains n integers a₁, a₂, ..., a_n (1 ≤ a₁, a₂, ..., a_n ≤ 10⁹).

The fourth line contains n integers b₁, b₂, ..., b_n (1 ≤ b₁, b₂, ..., b_n ≤ 10⁹).

The fifth line contains n integers c₁, c₂, ..., c_n (1 ≤ c₁, c₂, ..., c_n ≤ 10⁹).

The sixth line contains n integers d₁, d₂, ..., d_n (1 ≤ d₁, d₂, ..., d_n ≤ 10⁹).

Output:

Print the minimum amount of time Scott needs to get to the Cross while visiting each chair exactly once.

Sample Input:

7 4 3
8 11 12 16 17 18 20
17 16 20 2 20 5 13
17 8 8 16 12 15 13
12 4 16 4 15 7 6
8 14 2 11 17 12 8

Sample Output:

Note:

In the sample testcase, an optimal solution would be 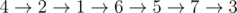$\text{[math]}$ . Spent time would be 17 + 24 + 23 + 20 + 33 + 22 = 139.

Informação

Provedor Codeforces

Código CF704B