Preparando MOJI
Bash got tired on his journey to become the greatest Pokemon master. So he decides to take a break and play with functions.
Bash defines a function f0(n), which denotes the number of ways of factoring n into two factors p and q such that gcd(p, q) = 1. In other words, f0(n) is the number of ordered pairs of positive integers (p, q) such that p·q = n and gcd(p, q) = 1.
But Bash felt that it was too easy to calculate this function. So he defined a series of functions, where fr + 1 is defined as:
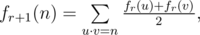
Where (u, v) is any ordered pair of positive integers, they need not to be co-prime.
Now Bash wants to know the value of fr(n) for different r and n. Since the value could be huge, he would like to know the value modulo 109 + 7. Help him!
The first line contains an integer q (1 ≤ q ≤ 106) — the number of values Bash wants to know.
Each of the next q lines contain two integers r and n (0 ≤ r ≤ 106, 1 ≤ n ≤ 106), which denote Bash wants to know the value fr(n).
Print q integers. For each pair of r and n given, print fr(n) modulo 109 + 7 on a separate line.
5
0 30
1 25
3 65
2 5
4 48
8
5
25
4
630
Informação
Provedor Codeforces
Código CF757E
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 09:11:53
Relacionados