Varying Kibibits

3000ms

262144K

Description:

You are given n integers a₁, a₂, ..., a_n. Denote this list of integers as T.

Let f(L) be a function that takes in a non-empty list of integers L.

The function will output another integer as follows:

First, all integers in L are padded with leading zeros so they are all the same length as the maximum length number in L.
We will construct a string where the i-th character is the minimum of the i-th character in padded input numbers.
The output is the number representing the string interpreted in base 10.

For example f(10, 9) = 0, f(123, 321) = 121, f(530, 932, 81) = 30.

Define the function

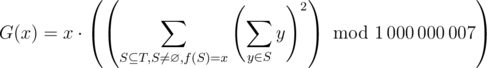
$\text{[math]}$ Here, $\text{[math]}$ denotes a subsequence.

In other words, G(x) is the sum of squares of sum of elements of nonempty subsequences of T that evaluate to x when plugged into f modulo 1 000 000 007, then multiplied by x. The last multiplication is not modded.

You would like to compute G(0), G(1), ..., G(999 999). To reduce the output size, print the value 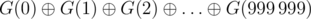$\text{[math]}$ , where $\text{[math]}$ denotes the bitwise XOR operator.

Input:

The first line contains the integer n (1 ≤ n ≤ 1 000 000) — the size of list T.

The next line contains n space-separated integers, a₁, a₂, ..., a_n (0 ≤ a_i ≤ 999 999) — the elements of the list.

Output:

Output a single integer, the answer to the problem.

Sample Input:

3
123 321 555

Sample Output:

292711924

Sample Input:

1
999999

Sample Output:

997992010006992

Sample Input:

10
1 1 1 1 1 1 1 1 1 1

Sample Output:

Note:

For the first sample, the nonzero values of G are G(121) = 144 611 577, G(123) = 58 401 999, G(321) = 279 403 857, G(555) = 170 953 875. The bitwise XOR of these numbers is equal to 292 711 924.

For example, 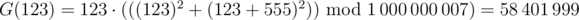$\text{[math]}$ , since the subsequences [123] and [123, 555] evaluate to 123 when plugged into f.

For the second sample, we have 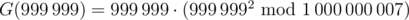$\text{[math]}$

For the last sample, we have 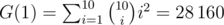$\text{[math]}$ , where 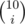$\text{[math]}$ is the binomial coefficient.

Informação

Provedor Codeforces

Código CF772D