Noise Level

The Berland's capital has the form of a rectangle with sizes n × m quarters. All quarters are divided into three types:

• regular (labeled with the character '.') — such quarters do not produce the noise but are not obstacles to the propagation of the noise;
• sources of noise (labeled with an uppercase Latin letter from 'A' to 'Z') — such quarters are noise sources and are not obstacles to the propagation of the noise;
• heavily built-up (labeled with the character '*') — such quarters are soundproofed, the noise does not penetrate into them and they themselves are obstacles to the propagation of noise.

A quarter labeled with letter 'A' produces q units of noise. A quarter labeled with letter 'B' produces 2·q units of noise. And so on, up to a quarter labeled with letter 'Z', which produces 26·q units of noise. There can be any number of quarters labeled with each letter in the city.

When propagating from the source of the noise, the noise level is halved when moving from one quarter to a quarter that shares a side with it (when an odd number is to be halved, it's rounded down). The noise spreads along the chain. For example, if some quarter is located at a distance 2 from the noise source, then the value of noise which will reach the quarter is divided by 4. So the noise level that comes from the source to the quarter is determined solely by the length of the shortest path between them. Heavily built-up quarters are obstacles, the noise does not penetrate into them.

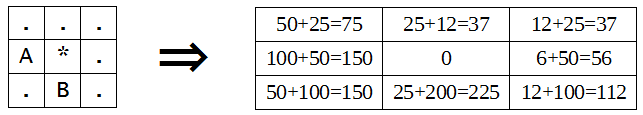The values in the cells of the table on the right show the total noise level in the respective quarters for q = 100, the first term in each sum is the noise from the quarter 'A', the second — the noise from the quarter 'B'.

The noise level in quarter is defined as the sum of the noise from all sources. To assess the quality of life of the population of the capital of Berland, it is required to find the number of quarters whose noise level exceeds the allowed level p.