Preparando MOJI
Nagini, being a horcrux You-know-who created with the murder of Bertha Jorkins, has accumulated its army of snakes and is launching an attack on Hogwarts school.
Hogwarts' entrance can be imagined as a straight line (x-axis) from 1 to 105. Nagini is launching various snakes at the Hogwarts entrance. Each snake lands parallel to the entrance, covering a segment at a distance k from x = l to x = r. Formally, each snake can be imagined as being a line segment between points (l, k) and (r, k). Note that k can be both positive and negative, but not 0.
Let, at some x-coordinate x = i, there be snakes at point (i, y1) and point (i, y2), such that y1 > 0 and y2 < 0. Then, if for any point (i, y3) containing a snake such that y3 > 0, y1 ≤ y3 holds and for any point (i, y4) containing a snake such that y4 < 0, |y2| ≤ |y4| holds, then the danger value at coordinate x = i is y1 + |y2|. If no such y1 and y2 exist, danger value is 0.
Harry wants to calculate the danger value of various segments of the Hogwarts entrance. Danger value for a segment [l, r) of the entrance can be calculated by taking the sum of danger values for each integer x-coordinate present in the segment.
Formally, you have to implement two types of queries:
First line of input contains a single integer q (1 ≤ q ≤ 5·104) denoting the number of queries.
Next q lines each describe a query. Each query description first contains the query type typei (1 ≤ typei ≤ 2). This is followed by further description of the query. In case of the type being 1, it is followed by integers li, ri and ki (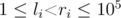
, - 109 ≤ ki ≤ 109, k ≠ 0). Otherwise, it just contains two integers, li and ri (1 ≤ li < ri ≤ 105).
Output the answer for each query of type 2 in a separate line.
3
1 1 10 10
1 2 4 -7
2 1 10
34
7
1 2 3 5
1 1 10 10
1 4 5 -5
2 4 8
1 1 10 -10
2 4 8
2 1 10
15
75
170
In the first sample case, the danger value for x-coordinates 1 is 0 as there is no y2 satisfying the above condition for x = 1.
Danger values for x-coordinates 2 and 3 is 10 + | - 7| = 17.
Danger values for x-coordinates 4 to 9 is again 0 as there is no y2 satisfying the above condition for these coordinates.
Thus, total danger value is 17 + 17 = 34.
Informação
Provedor Codeforces
Código CF855F
Tags
Submetido 0
BOUA! 0
Taxa de BOUA's 0%
Datas 09/05/2023 09:18:48
Relacionados