Mahmoud and Ehab and the function

2000ms

262144K

Description:

Dr. Evil is interested in math and functions, so he gave Mahmoud and Ehab array a of length n and array b of length m. He introduced a function f(j) which is defined for integers j, which satisfy 0 ≤ j ≤ m - n. Suppose, c_i = a_i - b_i + j. Then f(j) = |c₁ - c₂ + c₃ - c₄... c_n|. More formally, 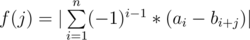$\text{[math]}$ .

Dr. Evil wants Mahmoud and Ehab to calculate the minimum value of this function over all valid j. They found it a bit easy, so Dr. Evil made their task harder. He will give them q update queries. During each update they should add an integer x_i to all elements in a in range [l_i;r_i] i.e. they should add x_i to a_{l_i}, a_{l_i + 1}, ... , a_{r_i} and then they should calculate the minimum value of f(j) for all valid j.

Please help Mahmoud and Ehab.

Input:

The first line contains three integers n, m and q (1 ≤ n ≤ m ≤ 10⁵, 1 ≤ q ≤ 10⁵) — number of elements in a, number of elements in b and number of queries, respectively.

The second line contains n integers a₁, a₂, ..., a_n. ( - 10⁹ ≤ a_i ≤ 10⁹) — elements of a.

The third line contains m integers b₁, b₂, ..., b_m. ( - 10⁹ ≤ b_i ≤ 10⁹) — elements of b.

Then q lines follow describing the queries. Each of them contains three integers l_i r_i x_i (1 ≤ l_i ≤ r_i ≤ n, - 10⁹ ≤ x ≤ 10⁹) — range to be updated and added value.

Output:

The first line should contain the minimum value of the function f before any update.

Then output q lines, the i-th of them should contain the minimum value of the function f after performing the i-th update .

Sample Input:

5 6 3
1 2 3 4 5
1 2 3 4 5 6
1 1 10
1 1 -9
1 5 -1

Sample Output:

Note:

For the first example before any updates it's optimal to choose j = 0, f(0) = |(1 - 1) - (2 - 2) + (3 - 3) - (4 - 4) + (5 - 5)| = |0| = 0.

After the first update a becomes {11, 2, 3, 4, 5} and it's optimal to choose j = 1, f(1) = |(11 - 2) - (2 - 3) + (3 - 4) - (4 - 5) + (5 - 6) = |9| = 9.

After the second update a becomes {2, 2, 3, 4, 5} and it's optimal to choose j = 1, f(1) = |(2 - 2) - (2 - 3) + (3 - 4) - (4 - 5) + (5 - 6)| = |0| = 0.

After the third update a becomes {1, 1, 2, 3, 4} and it's optimal to choose j = 0, f(0) = |(1 - 1) - (1 - 2) + (2 - 3) - (3 - 4) + (4 - 5)| = |0| = 0.

Informação

Provedor Codeforces

Código CF862E