Preparando MOJI

Paths

4000ms

524288K

Description:

You are given a positive integer n. Let's build a graph on vertices 1, 2, ..., n in such a way that there is an edge between vertices u and v if and only if 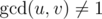$\text{[math]}$ . Let d(u, v) be the shortest distance between u and v, or 0 if there is no path between them. Compute the sum of values d(u, v) over all 1 ≤ u < v ≤ n.

The gcd (greatest common divisor) of two positive integers is the maximum positive integer that divides both of the integers.

Input:

Single integer n (1 ≤ n ≤ 10⁷).

Output:

Print the sum of d(u, v) over all 1 ≤ u < v ≤ n.

Sample Input:

Sample Output:

Sample Input:

Sample Output:

Note:

All shortest paths in the first example:

$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$

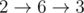
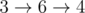
There are no paths between other pairs of vertices.

The total distance is 2 + 1 + 1 + 2 + 1 + 1 = 8.

Informação

Codeforces

Provedor Codeforces

Código CF870F

Tags

data structuresnumber theory

Submetido 0

BOUA! 0

Taxa de BOUA's 0%

Datas 09/05/2023 09:19:43

Relacionados

Nada ainda