Coloring a Tree

1000ms

262144K

Description:

You are given a rooted tree with n vertices. The vertices are numbered from 1 to n, the root is the vertex number 1.

Each vertex has a color, let's denote the color of vertex v by c_v. Initially c_v = 0.

You have to color the tree into the given colors using the smallest possible number of steps. On each step you can choose a vertex v and a color x, and then color all vectices in the subtree of v (including v itself) in color x. In other words, for every vertex u, such that the path from root to u passes through v, set c_u = x.

It is guaranteed that you have to color each vertex in a color different from 0.

You can learn what a rooted tree is using the link: https://en.wikipedia.org/wiki/Tree_(graph_theory).

Input:

The first line contains a single integer n (2 ≤ n ≤ 10⁴) — the number of vertices in the tree.

The second line contains n - 1 integers p₂, p₃, ..., p_n (1 ≤ p_i < i), where p_i means that there is an edge between vertices i and p_i.

The third line contains n integers c₁, c₂, ..., c_n (1 ≤ c_i ≤ n), where c_i is the color you should color the i-th vertex into.

It is guaranteed that the given graph is a tree.

Output:

Print a single integer — the minimum number of steps you have to perform to color the tree into given colors.

Sample Input:

6
1 2 2 1 5
2 1 1 1 1 1

Sample Output:

Sample Input:

7
1 1 2 3 1 4
3 3 1 1 1 2 3

Sample Output:

Note:

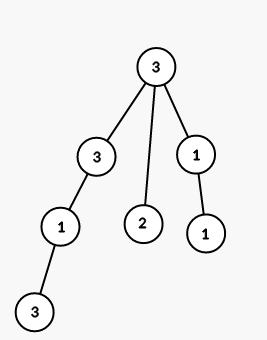
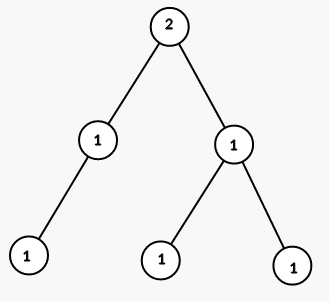
The tree from the first sample is shown on the picture (numbers are vetices' indices):

$\text{[math]}$

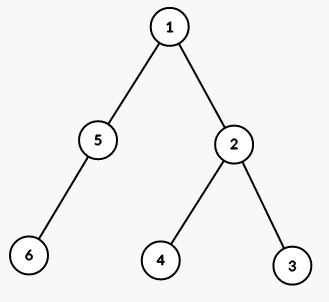
On first step we color all vertices in the subtree of vertex 1 into color 2 (numbers are colors):

$\text{[math]}$

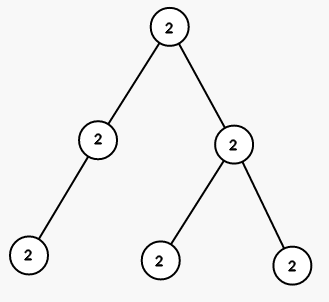
On seond step we color all vertices in the subtree of vertex 5 into color 1:

$\text{[math]}$

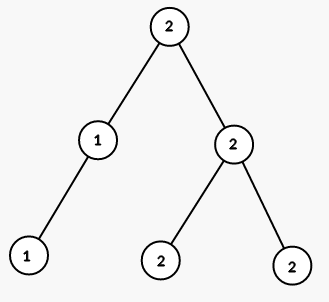
On third step we color all vertices in the subtree of vertex 2 into color 1:

$\text{[math]}$

The tree from the second sample is shown on the picture (numbers are vetices' indices):

$\text{[math]}$

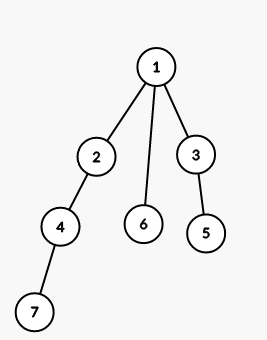
On first step we color all vertices in the subtree of vertex 1 into color 3 (numbers are colors):

$\text{[math]}$

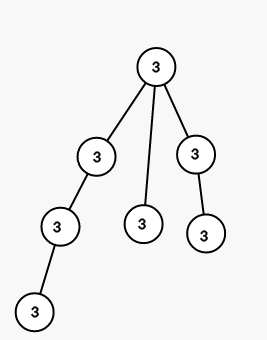
On second step we color all vertices in the subtree of vertex 3 into color 1:

$\text{[math]}$

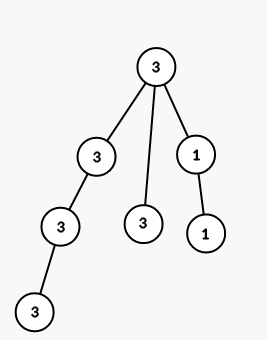
On third step we color all vertices in the subtree of vertex 6 into color 2:

$\text{[math]}$

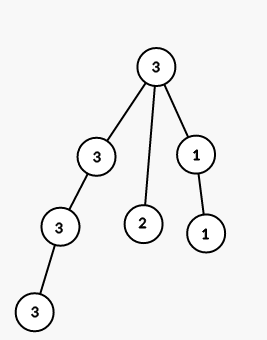
On fourth step we color all vertices in the subtree of vertex 4 into color 1:

$\text{[math]}$

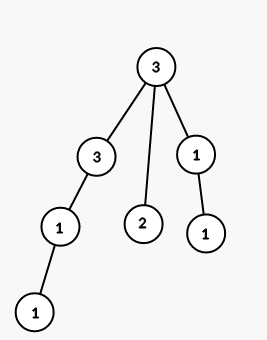
On fith step we color all vertices in the subtree of vertex 7 into color 3:

$\text{[math]}$

Informação

Provedor Codeforces

Código CF902B