New Year and Arbitrary Arrangement

2000ms

262144K

Description:

You are given three integers k, p_a and p_b.

You will construct a sequence with the following algorithm: Initially, start with the empty sequence. Each second, you do the following. With probability p_a / (p_a + p_b), add 'a' to the end of the sequence. Otherwise (with probability p_b / (p_a + p_b)), add 'b' to the end of the sequence.

You stop once there are at least k subsequences that form 'ab'. Determine the expected number of times 'ab' is a subsequence in the resulting sequence. It can be shown that this can be represented by P / Q, where P and Q are coprime integers, and 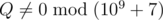$\text{[math]}$ . Print the value of $\text{[math]}$ .

Input:

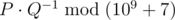The first line will contain three integers integer k, p_a, p_b (1 ≤ k ≤ 1 000, 1 ≤ p_a, p_b ≤ 1 000 000).

Output:

Print a single integer, the answer to the problem.

Sample Input:

1 1 1

Sample Output:

Sample Input:

3 1 4

Sample Output:

370000006

Note:

The first sample, we will keep appending to our sequence until we get the subsequence 'ab' at least once. For instance, we get the sequence 'ab' with probability 1/4, 'bbab' with probability 1/16, and 'aab' with probability 1/8. Note, it's impossible for us to end with a sequence like 'aabab', since we would have stopped our algorithm once we had the prefix 'aab'.

The expected amount of times that 'ab' will occur across all valid sequences is 2.

For the second sample, the answer is equal to 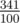$\text{[math]}$ .

Informação

Provedor Codeforces

Código CF908D