Don't Exceed

4000ms

262144K

Description:

You generate real numbers s₁, s₂, ..., s_n as follows:

s₀ = 0;
s_i = s_i - 1 + t_i, where t_i is a real number chosen independently uniformly at random between 0 and 1, inclusive.

You are given real numbers x₁, x₂, ..., x_n. You are interested in the probability that s_i ≤ x_i is true for all i simultaneously.

It can be shown that this can be represented as 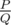$\text{[math]}$ , where P and Q are coprime integers, and 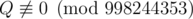$\text{[math]}$ . Print the value of P·Q^- 1 modulo 998244353.

Input:

The first line contains integer n (1 ≤ n ≤ 30).

The next n lines contain real numbers x₁, x₂, ..., x_n, given with at most six digits after the decimal point (0 < x_i ≤ n).

Output:

Print a single integer, the answer to the problem.

Sample Input:

Sample Output:

Sample Input:

1
0.50216

Sample Output:

342677322

Sample Input:

2
0.5
1.0

Sample Output:

623902721

Sample Input:

Sample Output:

859831967

Note:

In the first example, the sought probability is 1 since the sum of i real numbers which don't exceed 1 doesn't exceed i.

In the second example, the probability is x₁ itself.

In the third example, the sought probability is 3 / 8.

Informação

Provedor Codeforces

Código CF913H