Preparando MOJI
You're given a tree with n vertices rooted at 1.
We say that there's a k-ary heap of depth m located at u if the following holds:
Denote dpk(u) as maximum depth of k-ary heap in the subtree of u (including u). Your goal is to compute 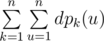 .
.
The first line contains an integer n denoting the size of the tree (2 ≤ n ≤ 3·105).
The next n - 1 lines contain two integers u, v each, describing vertices connected by i-th edge.
It's guaranteed that the given configuration forms a tree.
Output the answer to the task.
4
1 3
2 3
4 3
21
4
1 2
2 3
3 4
22
Consider sample case one.
For k ≥ 3 all dpk will be equal to 1.
For k = 2 dpk is 2 if 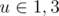 and 1 otherwise.
and 1 otherwise.
For k = 1 dpk values are (3, 1, 2, 1) respectively.
To sum up, 4·1 + 4·1 + 2·2 + 2·1 + 3 + 1 + 2 + 1 = 21.