k-substrings

4000ms

262144K

Description:

You are given a string s consisting of n lowercase Latin letters.

Let's denote k-substring of s as a string subs_k = s_ks_k + 1..s_{n + 1 - k}. Obviously, subs₁ = s, and there are exactly 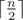$\text{[math]}$ such substrings.

Let's call some string t an odd proper suprefix of a string T iff the following conditions are met:

|T| > |t|;
|t| is an odd number;
t is simultaneously a prefix and a suffix of T.

For evey k-substring (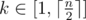 $\text{[math]}$ ) of s you have to calculate the maximum length of its odd proper suprefix.

Input:

The first line contains one integer n (2 ≤ n ≤ 10⁶) — the length s.

The second line contains the string s consisting of n lowercase Latin letters.

Output:

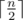Print $\text{[math]}$ integers. i-th of them should be equal to maximum length of an odd proper suprefix of i-substring of s (or - 1, if there is no such string that is an odd proper suprefix of i-substring).

Sample Input:

15
bcabcabcabcabca

Sample Output:

9 7 5 3 1 -1 -1 -1

Sample Input:

24
abaaabaaaabaaabaaaabaaab

Sample Output:

15 13 11 9 7 5 3 1 1 -1 -1 1

Sample Input:

19
cabcabbcabcabbcabca

Sample Output:

5 3 1 -1 -1 1 1 -1 -1 -1

Note:

The answer for first sample test is folowing:

1-substring: bcabcabcabcabca
2-substring: cabcabcabcabc
3-substring: abcabcabcab
4-substring: bcabcabca
5-substring: cabcabc
6-substring: abcab
7-substring: bca
8-substring: c

Informação

Provedor Codeforces

Código CF961F