Cycles in product

7000ms

262144K

Description:

Consider a tree (that is, an undirected connected graph without loops) $$$T_1$$$ and a tree $$$T_2$$$. Let's define their cartesian product $$$T_1 \times T_2$$$ in a following way.

Let $$$V$$$ be the set of vertices in $$$T_1$$$ and $$$U$$$ be the set of vertices in $$$T_2$$$.

Then the set of vertices of graph $$$T_1 \times T_2$$$ is $$$V \times U$$$, that is, a set of ordered pairs of vertices, where the first vertex in pair is from $$$V$$$ and the second — from $$$U$$$.

Let's draw the following edges:

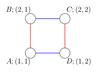
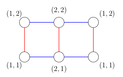
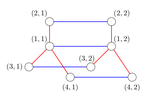
Between $$$(v, u_1)$$$ and $$$(v, u_2)$$$ there is an undirected edge, if $$$u_1$$$ and $$$u_2$$$ are adjacent in $$$U$$$.
Similarly, between $$$(v_1, u)$$$ and $$$(v_2, u)$$$ there is an undirected edge, if $$$v_1$$$ and $$$v_2$$$ are adjacent in $$$V$$$.

Please see the notes section for the pictures of products of trees in the sample tests.

Let's examine the graph $$$T_1 \times T_2$$$. How much cycles (not necessarily simple) of length $$$k$$$ it contains? Since this number can be very large, print it modulo $$$998244353$$$.

The sequence of vertices $$$w_1$$$, $$$w_2$$$, ..., $$$w_k$$$, where $$$w_i \in V \times U$$$ called cycle, if any neighboring vertices are adjacent and $$$w_1$$$ is adjacent to $$$w_k$$$. Cycles that differ only by the cyclic shift or direction of traversal are still considered different.

Input:

First line of input contains three integers — $$$n_1$$$, $$$n_2$$$ and $$$k$$$ ($$$2 \le n_1, n_2 \le 4000$$$, $$$2 \le k \le 75$$$) — number of vertices in the first tree, number of vertices in the second tree and the cycle length respectively.

Then follow $$$n_1 - 1$$$ lines describing the first tree. Each of this lines contains two integers — $$$v_i, u_i$$$ ($$$1 \le v_i, u_i \le n_1$$$), which define edges of the first tree.

Then follow $$$n_2 - 1$$$ lines, which describe the second tree in the same format.

It is guaranteed, that given graphs are trees.

Output:

Print one integer — number of cycles modulo $$$998244353$$$.

Sample Input:

2 2 2
1 2
1 2

Sample Output:

Sample Input:

2 2 4
1 2
1 2

Sample Output:

Sample Input:

Sample Output:

Sample Input:

Sample Output:

Note:

The following three pictures illustrate graph, which are products of the trees from sample tests.

In the first example, the list of cycles of length $$$2$$$ is as follows:

«AB», «BA»
«BC», «CB»
«AD», «DA»
«CD», «DC»

$\text{[math]}$ $\text{[math]}$ $\text{[math]}$

Informação

Provedor Codeforces

Código CF997D